Parece una contradicción, pero no lo es.
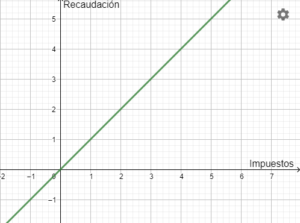
Se suele pensar que aumentando los impuestos se recauda más dinero y que reduciéndolos se recauda menos, podría parecer que lo lógico es por tanto que la gráfica fuera algo así:
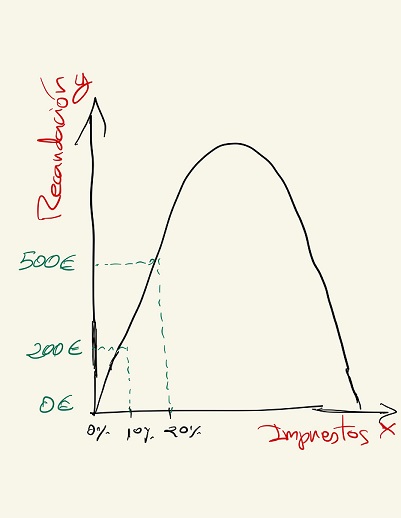
Pero según Arthur Laffer, la curva que mejor lo representa es esta (conocida como la curva de Laffer).
Lo que la curva de Laffer indica es que:
- Si el tipo impositivo es del 0%, la recaudación es de 0€
- Si el tipo impositivo es del 100%, la recaudación es también 0€, normal porque si el 100% de nuestro salario se va en pagar impuestos, lo mejor es no molestarse y no ir a trabajar ni emprender nada.
Todo lo que sea irnos a la derecha del punto con derivada cero de la función -máximo en este caso- implica que la gente no va a trabajar o si lo hace va a ser desmotivada o en economía sumergida.
Por ello, una vez que se sobrepasa el máximo de la función, seguir incrementando los impuestos no sirve de nada, es más, es contraproducente, la gente no va a producir más, no va a destinar dinero a invertir en mejoras o innovar.
El máximo de esa función es el punto óptimo al que subir los impuestos para conseguir la mayor recaudación fiscal.
A menos impuestos se incrementa la motivación para trabajar duro y emprender negocios nuevos impulsando una economía más fuerte, además y ya como opinión propia, cuando se recaudan más impuestos de los estrictamente necesarios, generalmente los gobiernos malgastan ese dinero.
Resumiendo: La curva de Laffer nos enseña que aumentar los impuestos puede hacer reducir los ingresos del gobierno en lugar de incrementarlos. Se ve muy claro con la gasolina en la que aproximadamente el 50% de su precio son impuestos, cuando ésta se pone por las nubes, la gente trata de coger menos el coche y por tanto compra menos litros de combustible, lo que implica recaudar menos al venderse menos.
Lo mejor de todo es que esta teoría económica está basada en matemáticas, ya que se sustenta en el Teorema de Rolle.
El Teorema de Rolle dice que si una función f es continua en el intervalo cerrado [a,b], diferenciable en el intervalo abierto (a,b) y f (a) = f (b), entonces $\exists x \in (a,b) | f'(x)=0$
Un caso particular del teorema es el que encaja con la curva de Laffer
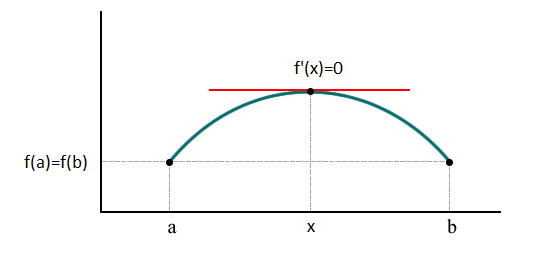
Pero puede haber «n» puntos en los que la derivada f'(x)= 0.
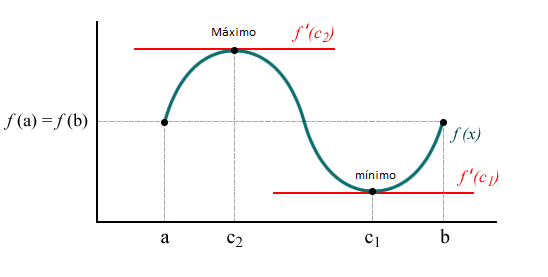
El fundamento matemático es el teorema de Rolle, el cual nos viene a decir que si el ingreso fiscal es una función continua del tipo impositivo, entonces tiene al menos un máximo -pues es una función que empieza creciendo- en un punto intermedio del intervalo -este punto no tiene por qué ser el centro exácto.