Las matemáticas están íntimamente unidas a las demostraciones, unas matemáticas sin demostración no serían matemáticas, las matemáticas van cogidas de la mano de estas, no se concibe una cosa sin la otra. Es lo que les da su principal característica: Rigor, robustez y confianza.
Siempre que demostramos algo seguimos los siguientes pasos: Primero, enunciamos unas hipótesis, que son una serie de condiciones previas que se sabe que son factibles, después enunciamos la tesis, que es el descubrimiento en sí (el resultado), y tras esto escribimos la demostración de la tesis, que son una serie de razonamientos que nos llevan desde la(s) hipótesis hasta la tesis a través de pasos que deben estar siempre bien justificados.
Hay muchos tipos de demostraciones. El pensamiento deductivo para hacer demostraciones se va adquiriendo poco a poco (como me gusta decir a mí, por sedimentación). El trabajo con demostraciones ayuda a desarrollar procesos como la abstracción, el análisis, la síntesis, la clasificación, la particularización, la comparación o la generalización. La demostración es la cumbre de la argumentación racional.
Vamos a ver algunos tipos de técnicas que solemos utilizar los matemáticos para demostrar cosas:
En concreto vamos a hablar de:
- Demostrostraciones Geometricas
- Demostraciones Directas
- Demostracciones por Inducción
- Demostraciones por Reducción al Absurdo
Estas podríamos decir que son las más importantes, pero hay muchas más.
1 -Demostraciones Geométricas
Nos hacen ver las cosas de una forma sencilla. Estas son las más sencillas.
1.1 -Demostración de que el área del triángulo es $\frac{b\cdot h}{2}$
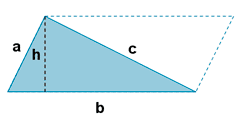
Con el dibujo se ve claro, sobran las palabras.
1.2 -Demostración del cálculo del área de un rombo
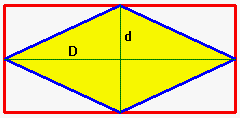
El área de un rombo es la mitad que la del rectángulo que le contine, es decir $A=\frac{D \cdot d}{2}$
Esta demostración es muy parecida a la anterior.
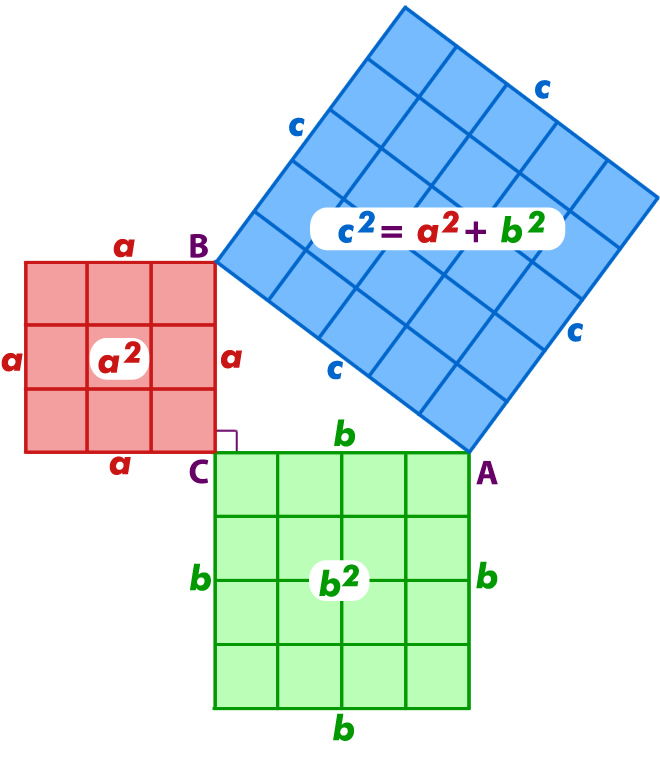
1.3 -Demostración del teorema de Pitágoras
De este teoréma hay muchísimas demostraciones, el motivo es que en la Edad Media se exigía una nueva demostración del teorema para alcanzar el grado de «Magister matheseos», en el libro The Pythagorean Proposition de E. S. Loomis aparecen 367 pruebas diferentes, veamos aquí una de ellas (la imagen que da comienzo a este artículo es otra demostración geométrica del teorema de Pitágoras).
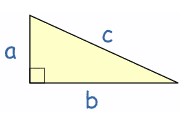
En un triángulo rectángulo $a^2+b^2=c^2$
Vamos a demostrarlo utilizando una figura geométrica y álgebra.

El área del cuadrado grande es lado x lado, i.e.,$(a+b)(a+b)$
El área del cuadrado pequeño (interior) es $c^2$
Vamos a calcular ahora el área de los triángulos (ya demostramos en el punto 1.1. que era base por altura dividido entre dos)
Área de cada triángulo $A=\frac{b \cdot a}{2}$
El área del cuadrado grande = área del cuadrado pequeño + área de los cuatro triángulos
$(a+b)(a+b)=c^2 + 4(\frac{b \cdot a}{2})$
$a^2+b^2+\cancel{2ab} = c^2 + \cancel {2ab}$
Ya lo tenemos.
Otra demostración muy visual y que a mí me gusta mucho se puede ver en este enlace de Youtube.
1.4 -Demostración de la identidad notable del binomio al cuadrado
$(a+b)^2 = a^2+b^2+2ab$
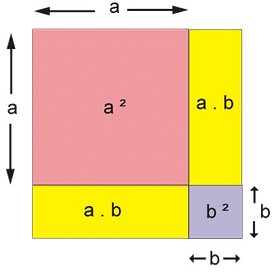
Otra forma más fácil sería desarrollando el lado izquierdo de la ecuación.
$(a+b)^2=(a+b)(a+b)=aa+ab+ba+bb= a^2+b^2+2ab$
1.5 -La suma de los ángulos de un triángulo suman 180º

2 -Demostraciones Directas
El camino por realizar consiste en, a partir de la hipótesis, encontrar una forma de llegar a la tesis utilizando las reglas que conocemos.
$\bullet \text{ Si } a,b\in\mathbb{R}, a,b>0 \text{ y }a \le b \text{ probar que } \frac{1}{a} \ge \frac{1}{b} $
Partimos de $a \le b$, como $a, b>0$ podemos dividir sin miedo la inecuación entre el producto de ambos.
$\frac{a}{ab} \le \frac{b}{ab}$
$\frac{1}{b} \le \frac{1}{a} \Leftrightarrow \frac{1}{a} \ge \frac{1}{b} $
$\bullet \text{ Si } x \text { es un número entero impar, entonces } x^2 \text{ es impar}$
Si x es impar, entonces podemos ponerlo de la forma x=2k+1 para algún entero k
$x^2=(2k+1)^2=(2k+1)(2k+1)=4k^2+4k+1=2(2k^2+2k)+1$
Sea $p=2k^2+2k$
$x^2=2p+1$, i.e, impar.
$\bullet \text{ La derivada del seno es el coseno}$
$(\sin x)´ =\lim \frac{\sin (x+h)-\sin (x)}{h} = \lim \frac{\sin(x)\cos(h)+\cos(x)sin(h) -\sin (x)}{h} = \lim \frac{\sin(x) (\cos(h)-1) + \cos(x)\sin(h) }{h} = \cos(x)$
$\bullet \text{ ¿Es 0.9999999999…= 1?} $
Podríamos pensar que no, que falta «un poquito» para ser iguales. De hecho, la mayoría de la gente piensa que no, pero lo que demostremos en matemáticas va a misa y sí, son lo mismo.
Sea $x = 0,\overline{9}$
Multiplicamos ambos lados de la igualdad por el mismo número (10).
10x = 9,9999999…
Restamos
10x – x = 9,9999999… – 0,9999999…
9x = 9
x = 1
Otra forma más sencilla de verlo sería:
$\frac{1}{3} = 0,33333…$
Si multiplicamos por 3 ambos lados, ya lo tenemos 1 = 0,99999…
2.1 -Ejemplos de Trigonometria.
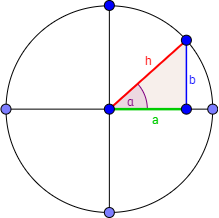
$\bullet \text{ Identidad trigonométrica elemental. } \cos^2 x + \sin^2 x = 1$
$\cos^2 x + \sin^2 x = (\frac{a}{h})^2 + (\frac{b}{h})^2 =\frac{a^2}{h^2}+\frac{b^2}{h^2}=\frac{1}{h^2}(a^2+b^2)=\text{ aplicando Pitágoras } \frac{h^2}{h^2} =1$
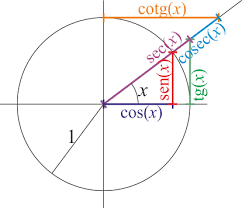
$\bullet \text{ Secante al cuadrado. Vamos a demostrar que } \sec^2 x = 1 + \tan^2 x$
Vamos a desarrollar el lado derecho de la ecuación, pero antes recordemos tres cosas:
$\sin^2 x + \cos^2 x = 1$
$\tan x = \frac{\sin x}{\cos x}$
$\sec x = \frac{1}{\cos x}$
Veamos
$1 + \tan^2 x = 1 + (\frac{\sin x}{\cos x})^2 = \frac{\cos^2 x +\sin^2 x }{\cos^2 x } = \frac{1}{\cos^2 x} = \sec^2 x$
Hay ejemplos muy buenos de demostraciones de trigonometría en matesfacil.com
Otros ejemplos:
$\bullet \text{ La solución a una ecuación de segundo grado } ax^2 + bx + c = 0 \text{, siendo a, b y c números reales es } \frac{-b\pm\sqrt{b^2-4ac}}{2a}$
Pongamos
$ax^2 + bx =-c $
y multipliquemos ambos lados por 4a
$4a^2x^2 + 4abx +b^2 = -4ac + b^2$
Agrupamos
$(2ax+b)^2=b^2-4ac$
Despejando la x ya lo tenemos
$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$
$\bullet \text{ Logaritmo del producto. } \log_{b}(P \cdot Q) = \log_{b}P + \log_{b}Q$
Sea
$log_{b}(P) =x \Rightarrow P =b^x $
$log_{b}(Q) =y \Rightarrow Q =b^y$
Entonces
$ \log_{b}(P \cdot Q) = log_{b}(b^x \cdot b^y) = log_{b}(b^{x+y}) = x+y=\log_{b}P + \log_{b}Q$
3 -Demostración por Inducción
El método de la inducción es una de las armas más potentes que tienen las matemáticas:

Nos permite concluir que una estructura o patrón es válido para la totalidad de los números naturales basándonos únicamente en dos muestras de evidencia. Se verifican dos resultados y se es capaz de obtener una conclusión para la infinidad de los números naturales.
Se ha dado el caso de situaciones que utilizando un ordenador se han demostrado ciertas conjeturas para mil millones de casos y luego no han sido ciertas para todos los casos como se suponía.
¿Cómo podemos saber si una estructura se cumple para una infinidad de objetos?, veámoslo con un ejemplo.
Cuando se suman «n» números impares, podemos darnos cuenta de que al sumar los primeros de ellos siempre da como resultado $n^2$
$1+3=4=2^2$
$1+3+5=9=3^2$
$1+3+5+7=16=4^2$
Podemos pensar que
$1+3+5+…+(2n-1)=n^2$
Para probar que una propiedad P(n) se verifica $ \forall n \in \mathbf{N}$Es suficiente probar solo dos hechos:
- Si P(n) se cumple para n=1, es decir P(1) es verdadero
- Si se supone P(n) cierto para un número arbitrario n , entonces P(n+1) también es cierto.
Si se pueden establecer ambos hechos, será posible concluir que P(n) se verifica $ \forall n \in \mathbf{N}$
- Para n=1, $1=1^2$ lo cual es trivial.
- Supongamos que ahora la identidad es cierta para un número n cualquiera.
$1+3+5+…+(2n-1)=n^2$
El siguiente número impar que sigue a (2n-1) es (2n+1), poniendo este número a ambos lados de la igualdad tenemos:
$ 1+3+5+…+(2n-1)+(2n+1)=n^2+(2n+1) $
Lo de la derecha es una identidad notable, así que
$ 1+3+5+…+(2n-1)+(2n+1) =(n+1)^2 $ que es la propiedad P(n+1)
Es decir, si se cumple la propiedad para un número n cualquiera entonces se cumple también para el siguiente.
Lo hemos demostrado por inducción matemática.
Existen infinidad de ecuaciones del tipo $1+3+5+7+9+11=36=6^2$ , pero al haberlo demostrado, ya sabemos con absoluta certeza que esto va a ser cierto siempre.
4 -Demostración por Reducción al Absurdo

Consiste en probar que si cierta afirmación es falsa, llegamos una contradicción lógica, por tanto esa afirmación es verdadera.
Ejemplo 1.
$\bullet \text{ Si } n^2 \text{ es impar, entonces } n \text{ es impar. }$
Supongamos que $n^2$ es impar pero n es par.
Es decir, existen dos números enteros «k» y «l» tal que
$n^2 = 2k+1$ y $n=2l$
Entonces, si $n=2l $\Rightarro n^2 = 2l^2$ y por tanto
$2k+1=4l^2$
$1=4l^2-2k$
$1=2(2l^2-k)$
y como si «l» y «k» son enteros, entonces $2l^2-k$ también lo es (llamémosle «m»)
$1=2m$
Es decir, estamos diciendo que 1 es par y eso es una contradicción.
Ejemplo 2.
$\bullet \text{ Probemos que } \sqrt{2} \text{ es irracional.}$
Supongamos que $\sqrt{2}$ es un número racional, entonces podemos ponerle com $\sqrt{2}=\frac{a}{b}$ siendo a y b enteros distintos de cero sin factores comunes.
Entonces $\sqrt{2} \cdot b = a$
Elevando al cuadrado ambos lados
$2b^2=a^2$, esto quiere decir que a es par y por tanto lo podemos poner como $a=2c$, siendo c también entero.
Sustituyendo en la ecuación original tenemos
$2b^2=a^2=(2c)^2=4c^2$
$b^2=2c^2$
Entonces b tiene que ser par, $b^2$ se puede dividir por 2, entonces b es par.
Hemos llegado a que tanto «a» como «b» son pares, entonces comparten un factor común que es 2, esto contradice lo que hemos asumido de que no tenían factores comunes, así que $\sqrt{2}$ es irracional.