Artículos cortos …
Bayes y la esperanza de vida.
La esperanza de vida en España es de 83 años. Un malentendido muy extendido es que, si alguien tiene por ejemplo 75 años, se tienda a pensar que le quedan unos 8 años más de vida. Si echamos mano de las matemáticas, según el Teorema de Bayes -probabilidad condicionada-, que sirve para calcular la probabilidad de un suceso teniendo de antemano información previa del mismo, lo normal es que, si una persona ya ha llegado a los 75 años, pues que viva a lo mejor hasta los 90.
De hecho, la pregunta más adecuada sería preguntarse por la probabilidad de que llege a vivir hasta los 88 años -por poner un ejemplo- sabiendo que ya ha llegdo a las 75.
Anonimato en las encuestas
Cada vez es más habitual que se realicen encuestas para hacer todo tipo de estudios, lo que ocurre, es que cada vez más -y con razón- las personas somos más reacias a dar datos que a nuestro entender sean información personal, desde nuestro color favorito a cualquier cosa que se nos pueda ocurrir.
Veamos una técnica sencilla para obtener información íntima de una muestra de personas, sin comprometer la identidad de cada uno de los miembros.
Imaginemos que queremos conocer qué porcentaje de la población en un determinado barrio es homosexual. Pedimos a la persona a la que estamos encuestando que tire una moneda al aire y que únicamente él vea el resultado. Si sale Cara, el encuestado responderá honestamente a la pregunta, ¿ha mantenido relaciones homosexuales en el pasado? (S/N) y si sale Cruz tiene que responder que «Sí».
De esta forma, conseguimos que el encuestado se sienta libre de decir la verdad, sin miedo a que nadie pueda usar su respuesta con intenciones no deseadas, por lo que es de suponer que el encuestado dirá la verdad.
Supongamos que hacemos 2000 encuestas y 1140 son afirmativas.
Aproximadamente 1000 de las 2000 respuestas habrán sido «Sí» porque ha salido Cruz (el 50%) y 140 habrán contestado afirmativamente con sinceridad porque la moneda salió Cara.
Por tanto, las personas homosexuales de nuestra muestra son 140/1000, es decir, el 14%.
La Esperanza es importante
Naturalmente me estoy refiriendo a la esperanza matemática.
Primero de todos, recordemos lo que es la esperanza matemática. Llamamos esperanza matemática o símplemente esperanza de una variable aleatoria al valor medio de un fenómeno aleatorio (la media aritmética).
Cuando la variable aleatoria es discreta, la esperanza es igual a la suma de la probabilidad de cada posible suceso aleatorio multiplicado por el valor de dicho suceso.
Representa la cantidad que se «espera» como resultado de un experimento aleatorio. El valor que toma la esperanza matemática en algunos casos puede no ser el «esperado» -el valor de la esperanza puede ser improbable o incluso imposible.
Por ejemplo, el valor esperado cuando tiramos un dado es 3,5.
$E(X)=1 \cdot \frac{1}{6} +2 \cdot \frac{1}{6} + 3 \cdot \frac{1}{6} +4 \cdot \frac{1}{6} +5 \cdot \frac{1}{6} +6 \cdot \frac{1}{6} =3,5$
Otro ejemplo más normal. Si 1/4 de las veces el valor que sale es el 2
1/3 el valor que sale es el 6
otro 1/3 de las veces sale el 15 y 1/12 sale un 54, el valor esperado es 12
$2 \cdot \frac{1}{4} + 6 \cdot \frac{1}{3} + 15 \cdot \frac{1}{3} +54 \cdot \frac{1}{12} + =12$
Una vez asentado este conocimiento, un simple ejemplo puede ser suficiente para darle la importancia que se merece a la Esperanza.
¿Cómo nos habrán hecho los análisis del Covid en el trabajo visto que se han limitado a decirnos “positivo o negativo” sin darnos mas información como podrían haber sido el número de anticuerpos en el caso de las empleados que ya lo hubieran pasado?
Desde un punto de vista puramente matemático (no quiero meter la pata y que algún médico me diga …no se puede hacer así por esto y por esto otro) se debería haber utilizado el concepto de esperanza matemática.
Pensemos que el laboratorio sospecha que el Covid lo va a tener una persona de cada 100 -por poner un número redondo y que se entienda el concepto mejor-. ¿Y si en lugar de analizar la sangre de cada uno por separado, el laboratorio mezclase las muestras de 50 y analizase esta mezcla en conjunto?. Si la muestra total da negativo, esos 50 están sanos y se ha hecho un único test, en caso contrario sí que tendría que analizar la sangre de cada una de las 50 personas por separado.
¿Cuál es el número esperado de tests (esperanza matemática) que tendría que realizar el laboratorio en caso de adoptar este procedimiento?.
1 análisis si el análisis de la mezcla da negativo.
51 análisis si el análisis de la mezcla da positivo.
La probabilidad de que un empleado esté sano es $\frac{99}{100}$ (casos favorables/posibles).
La probabilidad de que los 50 elegidos estén sanos y por tanto haya que realizar un único test es $50 \cdot \frac{99}{100}$.
La probabilidad de que por lo menos una persona tenga la enfermedad es el suceso complementario, i.e., $1- 50 \cdot \frac{99}{100}$, que es a su vez la probabilidad de que haya que realizar cincuenta y un tests.
Por tanto, el número esperado de análisis necesarios es (1 test × (99/100)50) + (51 tests × (1 – 50x(99/100)) = 21.
Siguiendo este procedimiento, la esperanza sería de hacer 21 tests por cada 50 empleados.
Nacimiento de la Probabilidad
Esta rama de las Matemáticas surgió en el siglo XVII de la mano de dos matemáticos franceses, Blaise Pascal y Pierre de Fermat y surgió porque ambos se pusieron a resolver un problema de la época que podríamos enunciar así:
Supongamos que dos personas están jugando a lanzar una moneda al aire, y el primero que acierte tres veces gana una cantidad de dinero, pero resulta que el juego se ve interrumpido cuando una persona gana por dos puntos a uno. Si no se pudiese continuar con el juego, ¿qué cantidad de dinero debería recibir de una forma justa cada jugador?
Antes de que Pascal y Fermat abordaran el problema, ya se habían propuesto diversas soluciones:
Podría dársele todo el dinero al que iba ganando pero podría ser injusto para el rival que tenía un punto, pues podría haber tenido la oportunidad de finalmente ganar. Otra posibilidad que puede parecer más justa es dividir el dinero en función del número de puntos ganados, de forma que el jugador que iba ganando conseguiría dos tercios del premio y el que iba perdiendo un tercio. Pero esto plantea un problema y es que si suponemos que la puntuación fuese de 1-0 en el momento de interrumpirse el juego, si se aplicase la misma regla, la persona con un punto recibiría todo el dinero, mientras que la otra persona no recibiría nada.
Pascal y Fermat encontraron una solución mejor y, al mismo tiempo con ello crearon una nueva rama de las Matemáticas.
Calcularon la probabilidad de que ganase cada persona. Para que ganase la persona que tenía un punto, tendría que conseguir otros dos puntos consecutivos, lo cual tiene una probabilidad de $\frac{1}{2} \cdot \frac{1}{2} =\frac{1}{4}$ por lo que debería recibir una cuarta parte del dinero y el resto debería ser para el que iba ganando.
Este mismo método puede aplicarse a cualquier otro problema de este tipo.
Cuando estudiaron este problema, Pascal y Fermat dieron con un concepto conocido como Esperanza Matemática -o Valor Esperado. En cualquier situación en la que esté implicada la probabilidad, el valor esperado es la media de lo que cabe esperar ganar de manera razonable.
Supongamos que jugamos a un juego en el que al tirar un dado ganamos 12€ si sacamos un 5. El valor esperado de este juego es de 2€, porque existe una probabilidad de $\frac{1}{6}$ de sacar un 5, y $\frac{1}{6}\cdot 12=2$. Si jugásemos muchas veces, ganaríamos por término medio 2€ en cada partida.
Después de jugar 100 veces, la cantidad media que ganaríamos seria de 200€, por lo que si nos costase 2€ jugar cada partida, acabaríamos más o menos igual -ni pérdidas ni ganancias.
Si jugásemos repetidamente, el valor esperado sería lo que esperamos ganar por término medio.
Sobres con dinero
Te dan a escoger entre dos sobres diciéndote que uno contiene el doble de dinero que el otro. Una vez abierto te dejarán cambiar al otro sobre si quieres. ¡Qué bien!, todas son ventajas…
Eliges el sobre I, lo abres y encuentras dentro 200€. Eso significa que en el sobre II hay 100 o 400€. Ahora te dicen que si quieres te dejan cambiar de sobre. Naturalmente piensas que tienes 200€ que ganar y 100 qué perder, así que como tienes Primaria aprobada aceptas el cambio…
Y yo me pregunto: ¿y por qué no has tomado el sobre II en primer lugar si sabes que te van a dejar cambiar?
«Siempre» elegiremos un sobre y cuando nos dejen cambiarlo lo haremos, y esto independientemente de la cantidad de dinero que contenga.
Regresión hacia la media
La regresión hacia la media gobierna el mundo.
Recordemos lo que es la regresión hacia la media, se trata del fenómeno estadístico según el cual, si una variable es extrema en su primera medición, esta tiende a estar más cerca de la media en su segunda medición y, si es extrema en su segunda medición, tiende a haber estado más cerca de la media en su primera.
Es decir, cuando en una medición obtenemos un valor extremo, lo normal es que en la siguiente medición obtengamos un valor cercano a la media.
Esto pasa en todos los ámbitos de la vida, si una película es un taquillazo, su segunda parte suele ser peor. Si una novela es un bestseller, su segunda parte suele ser peor, ¿por qué?, seguramente por la influencia de la regresión hacia la media.
Si disparamos con un arco a una diana y obtenemos una puntuación muy mala o incluso ni damos a esta, la siguiente vez que disparemos lo haremos mejor (estaremos más cerca de la media), la razón no es que nos hayamos convertido en buenos arqueros de repente, sino por la influencia de la regresión hacia la media.
Si inviertes en bolsa y se te da muy, muy mal, al siguiente intento seguramente lo harás mejor, no porque de repente te hayas convertido en un broker de los buenos, … es por la regresión hacia la media.
Se pueden encontrar ejemplos por todas partes, porque las matemáticas están en todas partes.
A veces las cosas son … lo que no parecen
$2^{99} \text{ vale solo la mitad que } 2^{100}$
Por cierto, un número grandísimo.
¿A qué distancia ha caído el rayo?
Siempre que vemos caer un rayo, la forma de saber si ha caído cerca o lejos de nosotros, es contar los segundos que transcurren desde que vemos el rayo y a posteriori oímos el trueno.
Como la velocidad del sonido es de 343 m/sg, la cuenta es muy fácil.
Si contamos 10 sg (un elefante, dos elefantes, tres elefantes, …10 elefantes) y consideramos la velocidad del sonido de unos 300 m/sg, el sonido ha tenido que recorrer 3000m, es decir, el rayo ha caído a 3 km de distancia. A correr…
No olvidarnos se seguir la regla 30/30 para protegernos de la caída de los rayos…
Nota: Las ondas como las del sonido o la luz -cualquier onda realmente- son perturbaciones que lo que hacen es trasladar energía de un sitio a otro y pueden viajar a través de diferentes medios como el aire o el agua. Todas las ondas se mueven a distintas velocidades según lo que estén atravesando, la velocidad máxima de la luz es de 300.000km/sg pero en el vacío. Las ondas sonoras viajan más rápido cuando viajan a través de cuerpos sólidos que cuando lo hacen a través de líquidos o de gases, por eso para saber si viene un tren lo detectas antes poniendo el oído en la vía que esperando a que el sonido te llegue a través del aire.
Una vez explicado esto, cuando he dicho que la velocidad del sonido es de 343 m/sg, claramente me estoy refiriendo a la velocidad a través del aire.
Fondo de inversión realmente bueno
Es seguro que algunos fondos se comportan bien por un largo periodo de tiempo como consecuencia del azar, o dicho de otra forma, algunos gestores de fondos aciertan durante un largo periodo de tiempo por pura casualidad.
De 500 fondos -o gestores-, es de suponer que aproximadamente 250 se comportarán bien durante el próximo año, únicamente como resultado de la buena suerte o la casualidad -tienen el 50% de probabilidades de portarse bien y el otro 50% de portarse mal. De éstos, igualmente podemos suponer que unos 125 se comportarán bien durante un segundo año. De estos 125, seguramente unos 62 se comporten bien otro año más, y así -«inducción»- podemos continuar con la misma idea de forma iterativa. El caso es que un fondo podría comportarse bien varios años seguidos únicamente como consecuencia del azar, y la prensa especializada diría que el gestor lo está haciendo fráncamente bien, cuando todo ha sido ventura.
El mercado es tan complejo, hay tantos datos y hechos con los que poder respaldar y justificar una cosa y la contraria en el mundo bursatil … olvidándo el azar…
¿Podrían malas decisiones económicas unidas entre sí ser capaces de proporcionarnos ganancias?.
Lo cierto es que es posible jugar a dos juegos que ocasionen pérdidas jugados de forma independiente, pero que, si alternativamente jugamos a uno y luego a otro, el resultado sea que acabemos ganando. Esto es lo que ocurre en la paradoja de Parrondo.
Juan Manuel Rodríguez Parrondo (9 de enero de 1964) es un físico español de la Universidad Complutense de Madrid que ideo el siguiente escenario que vamos a ver ahora en una versión simplificada:

Supongamos dos juegos, el juego A y el juego B.
En el juego A, se pierde 1€ en cada movimiento.
En el juego B, en cada movimiento se cuenta la cantidad de dinero que se tiene, si se trata de un número par se ganan 3€ y si se trata de un número impar se pierden 5€.
Supongamos que partimos con un saldo de 100€.
Si jugamos al juego A, está claro que en 100 movimientos perderíamos todo el dinero.
Si jugamos al juego B, también en 100 movimientos perderíamos todo el dinero.
¿Y si jugamos una vez al juego B y otra vez al juego A alternativamente?
| B | 100 | +3 | 103 |
| A | 103 | -1 | 102 |
| B | 102 | +3 | 105 |
| A | 105 | -1 | 104 |
| B | 104 | +3 | 107 |
| A | 107 | -1 | 106 |
| B | 106 | ||
| etc | etc |
Se ve claro que ganamos dinero -cada dos jugadas ganamos 2€. Los ejemplos de la paradoja de Parrondo son más complicados pero este nos vale para ver que la paradoja puede ocurrir.
Es decir, a pesar de que en cada juego por separado perderíamos seguro, si los alternamos, lo que ocurre en un juego afecta al otro, y la combinación de ambos provoca una ganancia segura.
A ver si soy capaz de dar con una cartera de fondos en la que aún cuando las cosas le vayan mal de forma individual a los subyacentes de esta, el fondo sin embargo me aporte beneficios …
Sergei Maslov ha publicado la demostración de cómo un inversor compartiendo capital entre dos bolsas de valores a la baja, obtiene un incremento de su capital en lugar de la pérdida esperada.
No salen las cuentas
Veamos un famoso problema de matemáticas.
Tres amigos deciden ir a comer a un restaurante en el que el menú cuesta 10€. Cuando terminan de comer, ponen 10€ cada uno y se lo dan al camarero, pero al mismo tiempo, uno de ellos le dice a este que conoce al dueño y que lo mismo les hace un descuento.
El camarero habla con su jefe y este decide descontar cinco euros de la cuenta, así que le da cinco euros para que se los devuelva.

Como dividir esos tres euros entre tres es un lío, el camarero decide devolver un euro a cada uno de los amigos y quedarse con 2€.
Por lo tanto, cada amigo ha pagado 9€.
9×3=27 + 2€ que se ha quedado el camarero = 29€
¿Pero no eran 30 euros lo que habían pagado?
.
.
.
.
.
Veamos cual es la explicación.
Los amigos pagan 27€.
El dueño pone 5€
El camarero se queda con 2€
27+5-2=30
¿Cuántos peces hay en un lago?
¿Cuántas hojas tiene un árbol?, ¿Cuántos conejos hay en el bosque?…
Aclaremos al principio de esta argumentación, que vamos a estimar, que no es lo mismo que contar, estimar nos da una idea aproximada pero no exacta de algo.
Una forma de estimar los peces que hay en un lago es la siguiente:
Suponemos que el número total de peces del lago es $t$
Pescamos $n$ peces -por ejemplo 1000, por hacerlo fácil-, los marcamos de alguna manera, por ejemplo los pintamos, y los devolvemos vivos al lago.
Esperamos unos días para que estos se vuelan a mezclar y repartir por todo el lago, y volvemos a pescar -usando la misma técnica anterior- $r$ peces -por ejemplo 1000 de nuevo- de los cuales observamos que $p$ están pintados -supongamos que son 10.
$p$ de cada $r$ peces están pintados -10 de cada 1000-, un 1% y hemos pintado 1000 así que 100.000 peces aproximadamente hay en el lago.

Matemáticamente sería:
$\frac{n}{t} \approx \frac{p}{r}$
Total de peces en el lago $t \approx \frac{r \cdot n}{p}$
Dinero y riesgo
¿Cuándo asumimos mayor riesgo con el dinero?
En general, la gente está más dispuesta a asumir mayor riesgo para evitar pérdidas económicas que para obtener ganancias.
Veámoslo con un ejemplo.
Supongamos que heredas 20.000€ de un tío lejano, pero en el testamento deja escrito lo siguiente:
Se te ofrece una de estas dos posibilidades:
a) Obtener 10.000€ más
b) Obtener 20.000€ más o nada en función de lo que salga al tirar un dado. Sale par: ganas los 20.000 euros y si sale impar no te llevas nada.
¿Qué elegirías?
La mayoría de la gente elegiría la primera opción.
Veamos el mismo caso desde otro punto de vista.
Heredas 40.000€ de un tío lejano, pero en el testamento deja escrito lo siguiente:
Se te ofrece una de estas dos posibilidades:
a) Devolver 10.000€
b) Devolver 20.000€ o nada en función de lo que salga al tirar un dado de forma similar al primer planteamiento.
¿Qué elegirías?
La mayoría de la gente elegiría la segunda opción para evitar tener pérdidas, pero si lo pensamos un poco nos daremos cuenta de que ambas opciones son idénticas.
Paradoja del cumpleaños
Esta paradoja dice que aunque no lo parezca, es muy probable que en un grupo de 23 personas (alumnos de una clase por ejemplo) haya dos de ellas que cumplan años el mismo día. Parece dificil puesto que el año tiene 365 día pero veamos que es cierto:
La probabilidad de que 2 personas tengan distinto cumpleaños es $\frac{364}{365}.
La de que 3 personas tengan distinto cumpleaños es $\frac{364}{365} \cdot \frac{363}{365}$
La de que 4 personas tengan distinto cumpleaños es $\frac{364}{365} \cdot \frac{363}{365} \cdot \frac{362}{365}$
.
.
La de que 23 personas tengan distinto cumpleaños es $P=\frac{364}{365} \cdot \frac{363}{365} \cdot \frac{362}{365} \cdot … \cdot \frac{343}{365}=0,492702766$
La probabilidad complementaria de que por lo menos dos personas tengan el mismo cumpleaños es $1-P=1-0,492702766=0,507297234=50,7\%$
Crecimiento exponencial
Ese concepto lo tiene claro menos gente de la que yo pensaba, repasémoslo.
La sucesión de números 2, 4, 8, 16, 32, 64, … tiene un crecimiento exponencial, mientras que la sucesión 2, 4, 6, 8, 10, 12, … tiene un crecimiento lineal.
Podemos decir que una sucesión crece exponencialmente -o geométricamente– si cada número de la sucesión se obtiene multiplicando el anterior por un factor/valor constante. Una sucesión crece linealmente -o aritméticamente– si si cada término de la sucesión se obtiene sumando la misma cantidad a su antecesor.
Por ejemplo, si metemos en un depósito 1000€ y en el banco nos dicen que nos van a dar un 10% anual (interés compuesto), el dinero crecerá cada año a razón de un factor 1,1 (o el 110%), al año tendremos 1.100€ (1000€ × 1,1), a los dos años tendremos 1.210€ (1.000€ × 1,1 × 1,1), y al cabo de x años el valor del depósito original será de 1.000€ × 1,1x (este es un crecimiento exponencial). Si ese mismo dinero lo hubiéramos metido en un depositado al 10% de interés simple, el valor del depósito inicial en los dos primeros años habría sido de 1.100€, 1.200€ y al cabo de x años tendríamos 1.000 + 100x (crecimiento lineal).
La idea del crecimiento exponencial viene muy bien explicada en la leyenda del nacimiento del ajedrez, un sabio inventó el ajedrez para que su rey pudiese pasar momentos amenos jugando y a éste le gustó tanto que le dijo que para agradecérselo le pidiese cualquier cosa y que el se lo concedería. El sabio le pidió algo que pudiera parecer algo sencillo y humilde, le pidió que por cada casilla del tablero de ajedrez, le diesen por la primera casilla un grano de trigo, por la segunda 2, por la tercera 4 y así sucesivamente duplicando la cantidad cada vez, de forma que por la última casilla le tendrían que dar 2 elevado a 63.
El rey aceptó y le ordenó al tesorero del reino que le pagase. Cuando el tesorero hizo los cálculos le dijo al monarca que habría que darle al sabio una cantidad de granos cuyo valor era superior a todos los activos del reino.
Claro, solo la última casilla es 9 223 372 036 854 775 808 que es una 400 veces la producción mundial de arroz de un año.
Información económica en la prensa
Ya vimos en la entrada ¿Para qué sirven las derivadas?, que las derivadas primera y segunda de una distancia o una altura, son o significan respectivamente su velocidad y su aceleración.
Cuando el comentarista de información económia de radio o prensa escrita informa de que un determinado índice económico sigue subiendo, pero no tan rápidamente como en el mes pasado, quizá no lo sepa (o quizá sí), pero lo que nos está diciendo es que la derivada primera del índice es positiva, pero la derivada segunda del índice es negativa. El índice está «llegando a un máximo».
¿Es lisa la Tierra?
Paseando por un centro comercial, pasé por la puerta de una bolera, el caso es que pensé que, con los golpes, esas bolas ya tenían imperfecciones, tenían pequeñas marcas, pero aun así todo el mundo las considerábamos lisas.
Me pregunté, ¿y cómo de lisa es entonces la Tierra?. Buscando en internet lo vi claro.
El diámetro de la Tierra es de 12.742 km y el punto más alto (imperfección en este caso) es el Everest que tiene 8,8 km de altura. El mar lo voy a considerar liso -porque en realidad es liso- aunque el punto más profundo tiene más o menos la misma profundidad que de altura el Everest.
$\frac{8,8}{12742}=0,000691$
Una bola de bolera tiene un diámetro de 218,3 mm, si consideramos que la máxima irregularidad pueda llegar a los 0,15mm, tenemos
$\frac{0,15}{218,3}=0,000687$
En proporción, la Tierra con sus montañas está tan lisa como una bola de bolera. ¡Qué curioso!, lo que se aprende en los centros comerciales.
Índice Bursátil
Cuando el comentarista de información económia de radio o prensa escrita informa de que un determinado índice económico sigue subiendo, pero no tan rápidamente como en el mes pasado, quizá no lo sepa, pero lo que nos está diciendo, es que la derivada primera del índice es positiva, pero la derivada segunda del índice es negativa. El índice está «llegando a un máximo».
Digitalización
Una foto de una mujer y un niño de pie frente al mar, ya no significa que esa mujer y ese niño hayan estado alguna vez juntos, ni frente al mar.
Deuda pública de un país
Cuando nos hablan de cifras realmente grandes, a mí me pasa que no sé muy bien realmente de que tamaño se está hablando, a veces veo en prensa el listado de las personas más ricas del mundo y mi cabeza no se imagina como de grande es ese dinero amontonado. Lo mismo me pasa con la publicación de la deuda pública de en mi país, España, en el momento de escribir estas líneas, su deuda pública es de 1,289 billones de euros, dividiéndolo entre el número de habitantes para ver a cuanto «tocamos», ya causa preocupación. Que ese número es muy grande está claro, pero ¿cómo visualizarlo para comprenderlo mejor? Una forma de visualizar dinero que le leí al matemático Ian Stewart es comparar euros -en su caso libras- con segundos.
Empecemos con un millón de euros.
Si tuviésemos que devolver un euro cada segundo, tendríamos que estar poniendo dinero durante 1.000.000/60/60/24 = 11,5 días.
En el caso de la deuda pública de España, siguiendo el mismo razonamiento, tendríamos que estar devolviendo un euro por segundo durante los próximos 40.874 años.
Saldaríamos la deuda en el año 42.894
Fracciones
Si le preguntas a un niño que qué es mayor si $\frac{2}{3}$ o $\frac{3}{5}$, lo más probable es que no sepa responderte. Pero si le preguntas que qué es lo que prefiere, 2 tartas a repartir entre 3 niños o 3 tartas a repartir entre 5, seguro que dirá que 2 tartas para 3 niños.
Correlación en Estadística
La correlación en estadística ya vimos en la entrada «Estadística y Fondos de Inversión» que significaba que dos o más cantidades estaban relacionadas de algún modo, pero ¡ojo!, no necesariamente significa que una sea causa de la otra. Muchas veces, las variaciones en las dos variables correlacionadas son el resultado de un tercer factor.”
Veamos un ejemplo:
Se ha hecho un estudio en el que nos dicen que los niños que tienen las manos más grandes tienen mejor ortografía, de aquí sacamos que hay una correlación entre tener las manos grandes y tener buena ortografía.
Esta extraña coclusión se explica fácilmente si pensamos que los niños que tienen las manos más grandes tienen mejor ortografía porque son mayores, siendo el factor edad la causa de que tengan las manos más grandes y de que su ortografía sea mejor.
Menos por Menos es Mas, ¿en serio?
¿Por qué un número negativo por un número negativo da un número positivo?, ¿pero en qué cabeza cabe?
No enseñaros la ley de los signos y claro, como es una ley no lo pusimos en duda
$+ \cdot + = +$
$+ \cdot – = -$
$- \cdot + = -$
$- \cdot – = +$
Si ya lo dice el dicho:
Los amigos de mis amigos son mis amigos
Los amigos de mis enemigos son mis enemigos
Los enemigos de mis amigos son mis enemigos
Y los enemigos de mis enemigos son mis amigos
Menos mal que en matemáticas se demuestra todo, veamos:
$(-1)(-1)=$
$(-1)(-1) + 0 \cdot 1 =$
$(-1)(-1) +((-1+1)\cdot 1) =$
$(-1)(-1) +(-1) \cdot 1 + 1 \cdot 1 =$
$(-1)(-1+1) + 1 \cdot 1=$
$(-1)\cdot 0 + 1 \cdot 1=$
$1\cdot 1$
Otra forma incluso más sencillo de demostrarlo es por Reducción al Absurdo:
Si pensamos que $(-1)(-1)=-1$, podemos dividir cada lado por –1 y acabar con la conclusión de que –1 = 1, que no tiene sentido. Por lo tanto, debemos llegar a la conclusión de que $(-1)(-1)$ es positivo.
Supongamos que quiero jugar a la Lotería Primitiva. ¿Qué opción es mejor?, ¿elegir yo los números o que los decida la máquina?.
La probabilidad de elegir unos números que resulten premiados, naturalmente es la misma en ambos casos, pero curiosamente, en la práctica salen más veces premiados los números que eligen las personas.
Pensemos en un caso muy sencillo para tratar de entender lo que pasa. En un pueblo muy pequeño, se juega a una lotería en la que el lotero saca al azar una bola de una cesta que contiene diez bolas numeradas del 1 al 10. El lotero saca un número de la cesta todos los domingos por la mañana. Únicamente dos vecinos apuestan cada semana. Tere elige siempre un número al alzar entre el 1 y el 10 mientras que Nicolás, siempre elige el 2, su número favorito. Con este planteamiento, el 2 será el número que más premios reparta. El motivo es que para que un número sea ganador deben darse dos condiciones:
a) Que el lotero lo saque del bombo.
b) Que algún jugador lo haya elegido.
Como Nicolás siempre elige el 2, la segunda condición se cumple siempre para el 2. No pasa lo mismo, por ejemplo, con el 7. El lotero podría sacar un 7 del bombo, pero es muy probable que Tere no lo haya elegido de modo que el 7 ganará muy pocas veces.
Aunque Tere y Nicolás tienen las mismas probabiidades de ganar, no todos los números tienen las mismas posibilidades de ser ganadores.
Ley de Murphy explicada con matemáticas
La famosa Ley de Murphy afirma que, por lo general, cualquier cosa que pueda salir mal saldrá mal.
Realmente, que las cosas no salgan bien no se debe a la mala suerte, sino a la complejidad e interdependencia de los sistemas hoy en día -el cuerpo humano y las enfermadades es otro ejemplo de sistema muy complejo. El que las cosas salgan mal puede explicarse la mayoría de las veces de una forma racional.
Hay un ejemplo particular de la Ley de Murphy que el científico Robert Matthews explica muy bien.
Supongamos que tenemos 10 pares de calcetines y que por lo que sea se nos pierden 6 de ellos haciendo la colada.
¿Qué resulta más probable, que tengamos suerte y acabemos con siete pares completos o que no tengamos suerte y terminemos con cuatro pares completos?. Según Murphy lo segundo.
Aplicando teoría de probabilidad, resulta que es más probable que al final nos quedemos con el peor resultado posible, sólo cuatro pares.
Por ejemplo, después de perder el primer calcetín, la probabilidad de que el segundo que se pierde deshaga otro par es de 18/19=0,94, frente a 1 /19=0,05 de que sea un calcetín del mismo par.
Es decir, no es la Ley de Murphy, en este caso son Matemáticas, pero la mayoría de las veces ocurre lo mismo, hay una explicación matemática, física o símplemente razonable de lo ocurrido.
Test de Turing
¿Pueden pensar las máquinas?, esta es la pregunta que en un principio quería responder Alan Turing con su famosa prueba, pero como definir la palabra «pensar» era muy complejo, la sustituyó por algo así como ¿puede una máquina tener buen desempeño imitando las respuestas que daría un humano? De hecho, su prueba en un principio la llamó «The imitation game» -como la película-, pero ahora es más conocido como el Test de Turing.
Desde que Alan Turing, la propuso, superarla ha sido considerada un hito en la Inteligencia Artificial.
La prueba consiste en una conversación entre un ser humano y una máquina que interactúan a través de un chat. La conversación debe ser en un lenguaje común y se tienen 5 minutos para que la máquina consiga engañar al humano y este piense que está chateando con otro humano.
Igual que el dietista que se lo pasa bien comiendo chocolate a escondidas, a mi me hacen reír las noticias sensacionalistas sobre IA que a veces salen en la prensa, aunque sea cierto que cada vez estamos más cerca de ver a una máquina superar la prueba. Una aplicación llamada Eugene, que imitaba a un niño, la superó en 2014, pero consiguió engañar al examinador porque un niño tiene menos vocabulario que un adulto.
El que un ordenador salga ganador en el test de Turing, lo único que demuestra es que los ordenadores pueden imitar el discurso de los humanos tan bien como para superar esa prueba bajo esas condiciones, pero eso no quiere decir que ese ordenador sea «inteligente». Al igual que hoy cuando tocamos una flor que pensábamos que era natural, al darmos cuenta de que es artificial decimos ¡anda, si es artificial!, en el futuro nos pasará lo mismo, tras mantener una larga conversación con lo que creeremos que es una persona, al abrir una puerta descubriremos con asombro que hemos estado charlando con un ordenador.
Falsos positivos Covid y Matemáticas.
Si damos positivo en un test de detección de Covid-19 realizada con un PCR -coger con un bastoncillo material genético del interior de la nariz para analizarlo- lo cierto es que es muy probable que se trate de un falso positivo. Veamos por qué:
Las pruebas PCR tienen una fiabilidad aproximada del 90%, es decir, si lo tienes dará positivo el 90% de las veces y si no lo tienes dará negativo el 90% de las veces.
La última estimación es que el 2% de la población mundial está infectada.
Imaginemos que vamos al médico, nos hacen el test y damos positivo. Pues yo me lo terminaría de creer si me hiciesen una segunda prueba, veamos por qué:
Supongamos que nos hacen el test a todos los empleados de la empresa en la que trabajo -somos 500 empleados.
En teoría el 2% de ellos, es decir, 10 empleados (0,02×500) lo tienen, pero como el 90% de los test darán positivo, de esos 10 empleados se «descubrirán» 9 de los casos (0.90×10).
Por otro lado, el 10% de los restantes 490 empleados, también darán positivo sin serlo, es decir, 49 empleados darán positivo.
Es decir, la foto es que tenemos 9+49=58 casos positivos cuando sólo 10 realmente lo son, por tanto, incluso si el test detecta el 90% de los casos, la mayoría de ellos son falsos positivos.
Tenemos un 17% ($\frac{10}{58}$) de probabilidades de tener el COVID habiendo dado positivo en el test.
La Falacia del Jugador
Empecemos diciendo que podemos describir una falacia como un argumento que puede parecer válido pero que, en realidad, no lo es.
La falacia del jugador es una falacia lógica por la que se cree equivocadamente pensando en términos de probabilidad, que los sucesos pasados afectan a los futuros. Comprende las siguientes ideas erróneas.
- Un suceso aleatorio tiene más probabilidad de ocurrir porque no ha ocurrido durante cierto período.
- Un suceso aleatorio tiene menos probabilidad de ocurrir porque ya ha ocurrido durante cierto período.
Por ejemplo, en el lanzamiento de una moneda en el que ya ha salido cinco veces seguidas cara, un jugador que razonase falazmente pensaría:
La probabilidad de obtener cara una vez es $\frac{1}{2}$
La probabilidad de que salga cara dos veces seguidas es $\frac{1}{2} \cdot \frac{1}{2}$
La probabilidad de que salga cara tres veces seguidas es $\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}$
y continuando con este razonamiento, el razonamiento erroneo pensaría que si ya ha salido cinco veces seguidas cara, la probabilidad de que vuelva a salir una sexta vez es $( \frac{1}{2})^6 $ que es poquísima. Aquí está el error.
Se trata de sucesos independientes. La probabilidad de obtener cara en un lanzamiento de moneda es de $ \frac{1}{2}$, siempre, se hagan los lanzamientos que se hagan, de hecho, nos sorprendería ver en series de lanzamientos de monedas muy largas como muchas veces hay rachas de muchas caras seguidas o muchas cruces seguidas.
Naturalmente esto es aplicable a los números que salen en el lanzamiento de un dado, a la lotería, etc.
Terremotos
Un terremoto de magnitud 8 no es el doble que un terremoto de magnitud 4, un terremoto de magnitud 8 es 10.000 veces mayor que un terremoto de magnitud 4., esto es así porque la escala sismológica es una escala logarítmica de base 10.
Que se trata de una escala logarítmica de base 10 significa que cada vez que subimos 1 grado en la escala, es como si multiplicáramos por 10. Es decir, que un terremoto de magnitud 4 tiene una magnitud 10 veces mayor que uno de magnitud 3, uno de magnitud 6 es 1000 veces mayor que uno de 7. Uno de magnitud 8 es 10.000 veces uno de magnitud 4. Este tipo de escalas, las logarítmicas, se utilizan cuando la el rango de valores que puede tomar el dato a medir es muy grande.
Ley de Benford
Esta ley lo que nos dice es que en gran variedad de conjuntos de datos numéricos que existen en la vida real, la primera cifra es 1 con mucha más frecuencia que el resto de los números. Es decir, los números suelen comenzar más frecuentemente por «1» que por cualquier otro dígito.
Hablemos un momento de logaritmos. Los logaritmos, nos permiten transformar operaciones complicadas en otras más sencillas: las multiplicaciones se transforman en sumas, las exponenciaciones en multiplicaciones, etc.
Por ello, antes de la llegada de los ordenadores eran muy usados y cualquiera que tuviera que realizar grandes cálculos solía pasar mucho tiempo consultando las tablas de logaritmos. Dichas tablas están ordenadas por el primer dígito del número del que queremos conocer su logaritmo. Así, si deseamos conocer el logaritmo de 136, buscaremos en las páginas del «1»
Una vez explicado esto, decir que en 1881, el matemático y astrónomo Simon Newcomb observó que las primeras páginas de las tablas de logaritmos que él y sus compañeros usaban estaban mucho más usadas que las finales, lo cual no tenía mucho sentido, porque los números consultados deberían tener una distribución más o menos uniforme y sería esperable que todas las páginas estuvieran igual de deterioradas. Dedujo que aparentemente los dígitos iniciales de los números no son equiprobables, sino que el 1 aparece como dígito inicial más frecuente, seguido del 2, etc. hasta el 9 que es el menos frecuente.
En 1938, y de manera independiente, el físico Frank Benford observó el mismo fenómeno en las tablas de logaritmos y realizó una comprobación empírica sobre un total de 20.229 números agrupados en 20 muestras de gran diversidad: áreas fluviales, magnitudes físicas y químicas, números de direcciones de personas, etc. A partir de estos enunciados, Benford postuló una ley que hoy en día se conoce como «ley de Benford».
En la actualidad se utiliza esta ley por ejemplo para encontrar engaños en las declaraciones de Hacienda.
Entscheidungsproblem
En 1928, el matemático David Hilbert, planteó lo que llamó el Entscheidungsproblem o «problema de la decisión». La pregunta era si siempre es posible encontrar un procedimiento para decidir, en un tiempo finito, si un enunciado matemático dado es verdadero o no. Esto podríamos verlo de otra forma, si existe un procedimiento para decidir si algo se puede o no demostrar. Hilbert pensaba que sí, pero estaba equivocado.
Kurt Gödel, cuya obra se ocupaba de los sistemas axiomáticos -reglas o axiomas que se consideran verdaderas- que pueden utilizarse para obtener teoremas, demostró muy pocos años después que en cualquier sistema axiomático lógicamente consistente, y suficientemente grande para abarcar todas las reglas de la aritmética, hay cosas necesariamente verdaderas, cuya verdad no puede demostrarse desde dentro del propio sistema. A esto se les llamó los teoremas de incompletitud de Gödel y esto implicaban que siempre habría algunas verdades matemáticas indemostrables. Esto fue verdaderamente un jarro de agua fría para los matemáticos.

¿Cuál es la cantidad mínima de aluminio necesario para fabricar una lata de Fanta de 330 ml?
Esto únicamente nos lo puede decir las matemáticas.
Recordemos la fórmula del volumen de un cilindro -lata de Fanta- que sería la superficie de la base o círculo $\pi r^2$ repetido continuamente durante toda la altura.
Es decir:
$ V= \pi r^2 h$

En nuestro caso, V=330ml que claramente depende del radio «r» y de la altura «h».
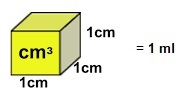
$V=330ml=330 cm^3$
Suponiendo que la lata tiene un grosor inapreciable y fijándonos únicamente en la superficie, vamos a calcular ésta.
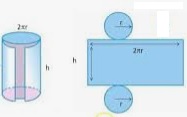
La superficie que tengo que calcular es la superficie de los dos círculos que forman la base y tapa de la lata (la superficie de una circunferencia es $\pi r^2 $) + la superficie del rectángulo (base x altura) que es todo el lateral de la lata (que es la longitud de la circunferencia $2 \pi r$) por la altura de la lata h.
Es decir, la Superficie de aluminio de la lata de Fanta es:
$S= 2(\pi r^2) + 2\pi r h$
Como tenemos que
$330=\pi r^2 h \Rightarrow h=\frac{330}{\pi r^2 }$
sustituyendo
$S= 2(\pi r^2) + 2\pi r \frac{330}{\pi r^2 }$
$S= 2(\pi r^2) + \frac{660}{r }$
Aquí ya tengo una función S que depende de una variable r, es decir tengo la función S(r) -estamos acostumbrados a llamar a las funciones f(x) pero esto es lo mismo- para la que quiero calcular en dónde tiene un mínimo absoluto.
Si recordamos a lo que vimos en el artículo sobre derivadas, los candidatos a mínimos relativos son aquellos puntos r que cumplan que la derivada primera de la función es igual a cero y la derivada segunda es positiva.
En nuestro caso además r>0 porque no tiene sentido una lata con un radio no positivo.
$S'(r)=0$
$2 \pi 2 r + 660 \frac{-1}{r^2} = 0$
$ 4 \pi r – \frac{660}{r^2} = 0$
$4 \pi r^3 -660=0$
$r=\sqrt[3]{\frac{660}{4 \pi}}$
Observar que «r» son cm, si hubiésemos estado usando todo el tiempo que el volumen fuesen $cm^3$, al llegar a este punto veríamos que estos se anularían con la raíz cúbica y se quedarían en $cm$.
Como la derivada segunda es
$S´´(r)=12 \pi r^2$ , se ve claro que la derivada segunda siempre va a ser positiva por lo que tenemos un mínimo para el «r» encontrado.
Teniendo el radio, podemos despejarlo en la fórmula de la altura que ya vimos que era:
$ h=\frac{330}{\pi r^2 } $
y así tener las dimensiones «r» y «h» de la lata que utiliza la menor cantidad de aluminio posible.
Las matemáticas son increibles.
¿Es el 1 un número primo?
El número 1 no se considera un número primo en contra de lo que mucha gente piensa, lo cierto es que podría serlo, pero esto complicaría varios teoremas existentes y realmente no nos conviene. El Teorema Fundamental de la Aritmética dice que todo número puede expresarse de forma única como un producto de uno o más números primos (sin tener en cuenta el orden).
Por ejemplo, 14 = 2 × 7 y 75 = 3 x 5 x 5. Si admitiésemos el 1 como un número primo, existirían infinitas maneras de expresar cualquiera de estos ejemplos, por centrarnos en el primero, podríamos decir:
14 = 2 × 7
14 = 2 x 7 x 1
14 = 2 x 7 x 1 x 1
14 = 2 x 7 x 1 x 1 x 1 etc
Como curiosidad respecto a los números primos, recordar que el mejor teorema sobre la distribución de los números primos se llama Teorema de los Números Primos. Lo que este teorema dice es que para cualquier número N que sea suficientemente grande, el número de primos inferiores a N es aproximadamente igual a $\frac{N}{ln(N)}$ . Como observación, decir que los huecos entre los números primos son mayores a medida que crece el tamaño de los números, Al principio están todos bastante juntitos 2,3,5, 7 … pero cada vez la distancia se va haciendo más grande.
El $\infty$ es un número muy grande. Leyenda urbana.
Hay una leyenda urbana o una tendencia a pensar, que el infinito es como un número muy grande y que el $5^{20}$ está más cerca del infinito que el número 1.
Lo cierto es que no es así. El hecho de escribir números cada vez más grandes no nos sitúa más cerca del infinito. Estamos tan lejos o tan cerca del infinito en el número 1 como en el número 10.000 o como en un gúgol -en ingles googol.
El infinito existe entre 0 y 1, por ejemplo, porque existen infinitas fracciones $\frac{1}{2} \frac{1}{3} \frac{1}{4} \frac{1}{5}$ , y así sucesivamente. No hay que confundir el infinito con un gran número finito. Para entender el infinito tenemos que olvidar y salirnos completamente del universo de los números finitos, así como utilizar estos como un apoyo para nuestra comprensión.
Georg Cantor fue la primera persona que formalizó la noción de infinito, la comunicad matemática se opuso a sus ideas y esto le afectó bastante, de hecho pasó los últimos días de su vida en un hospital psiquiátrico. El concepto de infinito en su época no se comprendía bien, había un solo infinito, pero Cantor reveló que había unos infinitos más grandes que otros, esto era una mezcla entre filosofía y teología para la época y fue un incomprendido. ¡Una lástima!…
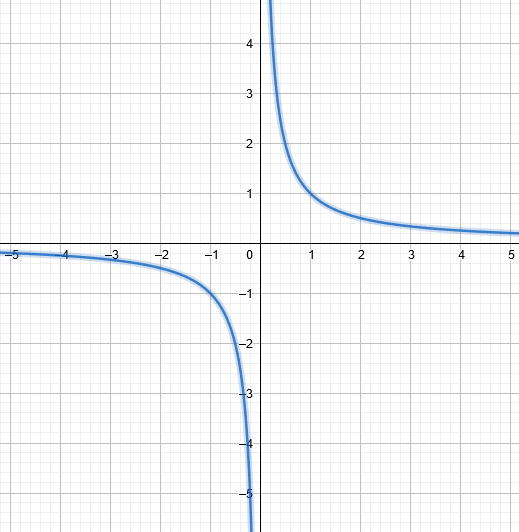
He preguntado a un compañero que qué era un Radián, a lo que me ha contestado con un mensaje con la siguiente imagen:
que es lo que mestra Google si escribes la palabra «radian». A mí esta explicación me resulta un poco «engorrosa».
Voy a explicarlo yo con otras palabras:
Un radián (rad) es una medida más de medición de ángulos igual que lo puede ser el grado sexagesimal. La cirunferencia tiene 360º (grados sexagesimales) o dicho de otra forma $2 \pi \cdot rad$. Veámoslo:
Un radián, es el ángulo que se forma si la longitud del radio -de una circunferencia- la sobreponemos sobre la circunferencia, el ángulo de ese «quesito» que sale es un radian. El segundo dibujo de la imagen anterior es muy bueno, pero el texto lo complica un poco.
Seguro que explicado así se entiende mejor.

$2 \pi rad =360º \Rightarrow 1 rad=\frac{180º}{\pi}$
Ningún número se puede dividir entre 0
En matemáticas no se puede dividir ningún número entre cero, $\frac{n}{0}$ es Indeterminación.
A veces hay gente que piena que por ejemplo, si dividimos $\frac{1}{0}$ eso da infinito, su argumento es que si te acercas mucho a cero con números cada vez más pequeños, el resultado es cada vez un número mas grande (tendiendo a infinito $\infty$). Lo que ocurre, es que no se dan cuenta de que eso es únicamente cierto si nos acercamos a cero con numeros positivos, porque si nos acercamos con números negativos el resultado es $-\infty$.
Si el valor del límite es diferente dependiendo de si nos acercamos por la derecha o por la izquierda, en ese caso decimos que el límite es «indeterminado».
Los físicos pasaron de tener al átomo como la partícula más pequeña de la que estaba formada la materia en el universo, a descubrir otras más pequeñas, los quarks, a los que ya se les considera indivisibles.
En Matemáticas siempre se ha considerado a los números primos como los «ladrillos» del universo matemático, los «átomos» de los físicos, en contraposición a los números compuestos, que son aquellos que se pueden factorizar en números primos. Pero entonces, ¿esto quiere decir que nuestros amigos físicos han llegado más lejos que los matemáticos al descubrir los quarks?.
Si nos limitamos a los números enteros, 2, 3, 5,… serán números primos siempre.
Utilizando números complejos (recordemos que $i=\sqrt{-1}$ ) podemos ver que no, nuestros amigos los físicos no han ido más lejos que los matemáticos, ya que ocurren cosas como estas:
$2=(1+i)\cdot(1-i)$
$5=(2+i)\cdot(2-i)$, pero también
$5 = (1 + 2i)\cdot(1 – 2i)$
$13 = (2 + 3i)\cdot(2 − 3i)$
$17 = (4 + i) \cdot(4 − i)$
$29=(2 + 5i)\cdot(2 − 5i)$
…
En teoría de conjuntos primitiva no solo podíamos tener cosas bien definidas como por ejemplo el consjunto de los números pares P={x : x es par} (: se lee «tal que»), también podíamos tener un conjunto de cosas abstractas, A = {x: x es una cosa abstracta}. En este caso A es en sí misma una cosa abstracta, por lo que podemos decir que A $\in$ A. Pero si permitiésemos esta relación en Matemáticas, surgirían problemas muy graves. De Bertrand Russell es la famosa idea de un conjunto S que contenía todas las cosas que no se contenían a sí mismas, es decir, S = {x: x $\notin$ x}.
Después se hizo la pregunta: «¿Es S $\in$ S?» Si la respuesta es «Sí», S tiene cumplir con la frase definitoria de S, y por lo tanto S $\notin$ S. Por otro lado, si la respuesta es «No» y S $\notin$ S, S no cumple con la relación definitoria de S = {x: x ∈$\notin$ x} y por consiguiente S $\in$ S. La pregunta de Russell acababa con esta afirmación, la base de la paradoja de Russell:
S $\in$ S si y solamente si S $\notin$ S.
A este tipo de paradojas se les denomina «antinomias» y hay que evitarlas. En matemáticas no se pueden tener sistemas que generen contradicciones. Russell creó una teoría de tipos dentro de la teoría de conjuntos y sólo permitió a $\in$ A si «a» era de un tipo inferior a A, evitando así expresiones como S $\in$ S.
Burro grande, ande o no ande.
Es habitual el dilema de si comprar una pizza de 40 cm de diámetro o dos de 24 cm.
En general, suele salir más barata una grande, pero es que además, si las imaginamos como el área de dos círculos.
Área de la pizza 40cm =$\pi\cdot R^2=\pi \cdot 20^2=\pi \cdot 400$
Área de 2 pizzas 24cm = $2 \cdot \pi\cdot r^2=2 \cdot \pi \cdot 12^2=2 \cdot \pi \cdot 144=\pi \cdot 288$
Sobran las palabras.
También es mejor una grande que dos medianas.

Podriamos haber hecho el cálculo mirando el volumen en lugar del área, pero no cambiaría nada porque el volumen sería Volumen=área x altura y en ambos casos la altura es la misma, por lo que no afectaría al cálculo.
Algo similar ocurre por ejemplo si nos dan a elegir entre comer 3 bolas de helado de 8cm de radio o 40 bolas de helado de 3cm de radio. La mayoría de la gente elegiría las 40 bolas de helado, cuando en realidad, las 3 bolas grandes tienen casi un 30% más de volumen.
Edad y Sistemas de Numeración.
Solemos marcar como momentos «críticos» en nuestras vidas aquellos en los que cumplimos años múltiplos de 10, por ejemplo, al cumplir los 30, 40, etc. Paparruchas, no tenemos de qué preocuparnos, veamos por qué:
Estamos acostumbrados a contar las cosas en un sistema numérico en base 10, pero nadie nos obliga a ello.
Los 30 años en un sistema de numeración en base 13 son 24 (2 veces 13 y 4veces 1).
Los 40 años en un sistema de numeración en base 13 son 31 (3veces 13 y 1 vez 1).
Si aun así, nos preocupa la edad que tenemos en base 13, podemos aumentar más la base usada e irnos por ejemplo al sistema hexadecimal.
Opiniones laborales
Viene un compañero y te dice que tal nuevo jefe es malo (o bueno), y además te dice que lo es por los motivos A, B, C y D. Matemáticamente hablando, la probabilidad de que esa opinión sea cierta es bastante baja. Veamos los motivos:
- No hace falta ser un lince en matemáticas para saber que una muestra de una persona no es estadísticamente fiable, al no ser representativa.
- La muestra se ha autoseleccionado… no pinta bien.
- Cuantos más detalles nos den, aunque la narración parezca más creíble, la probabilidad de que sea cierto $A \cap B \cap C \cap D$ es más difícil a que por ejemplo solo nos hubiesen facilitado los motivos $A \cap B$.
Hacer y Verificar.
Hacer y verificar son dos operaciones muy distintas: por ejemplo, es fácil verificar que 131 × 311 = 40.741, pero hallar dos factores de 3 cifras que den como resultado 40.741 ya es otro cantar.
Platón y el Mito de la Caverna
La idea sobre lo que realmente son las matemáticas está profundamente relacionada con el famoso Mito de la Caverna de Platón.
Platón imagina a un grupo de prisioneros que se encuentran encadenados desde niños detrás de un muro dentro de una caverna. Allí, un fuego ilumina al otro lado del muro y los prisioneros ven las sombras proyectadas por objetos que se encuentran sobre este muro.
Los prisioneros creen que aquello que observan es el mundo real.
Con esta alegoría, Platón duda de que la información que recibimos a través de nuestros sentidos sea el mundo real.
Digo que las matemáticas están relacionadas en cierto sentido con el Mito de la Caverna, porque las verdades matemáticas no son sólo las que hacen referencia a los triángulos, cálculos de áreas o polinomios que estudiamos en el colegio, sino a objetos abstractos que por nuestra limitación como humanos de no ver más que tres dimensiones, nos resultan imposibles de imaginar.
Galileo decía que «Las Matemáticas son el lenguaje con el que el Dios ha escrito el universo».
Yo humildemente me atrevo a decir algo más, una vez descubiertos -muchos años después de la muerte de éste genio- los conceptos de infinito y la geometría n-dimensional – que por cierto, tanto ayudó a Einstein en su Teoría de la Relatividad- las matemáticas abarcan mucho más que el mundo físico y universo que conocemos, se alejan libres de la realidad física que tanto han modelizado y todo un mundo abstracto sigue aún por descubrirse, esa son las verdaderas matemáticas.
Es típico que mucha gente se pregunte si no perdió el tiempo estudiando matemáticas en el instituto o en la universidad, cuando él lo que realmente quiere es ser arquitecto o ingeniero y los cálculos matemáticos ya se los hace el ordenador.
Yo considero que la mejor respuesta es esta:
Un deportista de élite como Rafa Nadal, no es uno de los mejores tenistas del mundo porque entrene mucho jugando al tenis, sino porque entrena sobre todo mucho en el gimnasio y además entrena jugando al tenis. Sin las horas de gimnasio, no realizaría saques a más de 200 km/h, no llegaría a todas las bolas, en definitiva, no tendría la forma física suficiente para poder jugar un tenis de primer nivel.
Pues las matemáticas, además de útiles en sí mismas, son el gimnasio necesario para poder sobresalir en otras disciplinas.
Optimismo en los fondos de inversión
Navegando por internet he llegado a una página en la que Morningstar nos muestra las rentabilidades de fondos por categorías en varios periodos de tiempo (https://www.morningstar.es/es/tools/categoryoverview.aspx) hasta aquí todo bien si no fuera porque creo que los resultados de los cálculos son más optimistas de lo que deberían. Lo he pensado debido a que los resultados me han parecido mejores de lo que esperaba encontrarme.
Imagino que el motivo es que se está calculando la rentabilidad acumulada de todos los fondos de una categoría y solo se está teniendo en cuenta aquellos que siguen “vivos” al final del periodo de cálculo -5 años por ejemplo-, ignorando aquellos que han desaparecido o han cesado en su cotización por «malillos», es decir, en cierto sentido se está haciéndo el cálculo, con los mejores.
Como hacer los cálculos teniendo en cuenta las bajas es bastante más complejo, «supongo» que no andaré muy descaminado.
No hacer nada vs hacer un poquito cada día
En un año:
Nada: 0 x 365 = 0
Un poquito cada día: 0,01 x 365 = 3,65