«Los Elementos de Euclides», es una colección de libros escritos por el matemático griego Euclides hacia el año 300 a. C. y son posiblemente los libros más famosos en la historia de las matemáticas. Definen lo que en el colegio y en el instituto hemos estudiado como la rama de geometría dentro de las matemáticas. A esta geometría se la llama Geometría Euclídea.
Euclides de Alejandría enumera cinco postulados, el quinto de los cuales dice:
«Por un punto exterior a una recta, se puede trazar una única recta paralela a la dada»
Pero, ¿y qué pasa si dudamos de lo que dice este postulado, que coincide con lo que nos indica el sentido común?
Pues que ocurren cosas maravillosas…
Generalizando, podemos decir que existen tres tipos de geometrías, que surgen a partir de la modificación o no de este quinto postulado:
a) Se acepta el postulado.
Por un punto exterior a una recta pasa una y sólo una recta paralela a ella. Esta es la geometría euclidiana, la del instituto, la geometría que encontramos en el plano. Se trata de una geometría con curvatura cero.
En la geometría euclídea, la suma de los ángulos de cualquier triángulo es siempre $180^{\circ}$.
Si negamos el postulado, nos quedan dos opciones:
b) Por un punto exterior a una recta pasan varias rectas paralelas a ella.
A esta geometría se le llama Geometría Hiperbólica. Tiene curvatura negativa y esta es la geometría que se da sobre la superficie de una Silla de Montar por ejemplo.
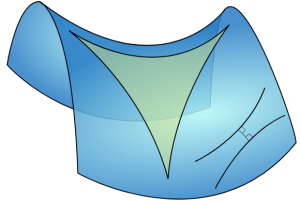
En la geometría hiperbólica, la suma de los ángulos de cualquier triángulo es siempre menor a $180^{\circ}$.
Una manera de visualizar esta geometría es utilizar el Modelo del Disco de Poincaré. Es un modelo en el que los puntos de la geometría están en un disco y en el que las líneas rectas son arcos de circunferencia contenidos en el disco. En otras palabras, consiste en la transformación del plano en un círculo de la siguiente forma.
Considerando esta inversión como la generalización de una reflexión con respecto a una línea recta, decimos que dos puntos P y P’ guardan una relación de inversión con respecto a la circunferencia de centro O y radio R cuando se cumple que:
- Los puntos P y P’ están sobre una misma semirecta con origen en O
- Sus distancias cumplen la igualdad:
$R^2=|\overline{OP}|\cdot |\overline{OP’}|$
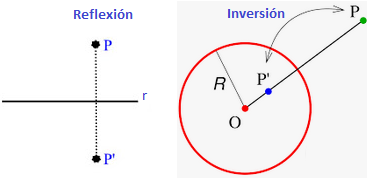
Dicho de una forma sencilla:
El punto P está reflejado debajo de la recta «r» poniendo un punto P’ por debajo de dicha recta que tenga la misma distancia a «r» como la distancia que tiene hasta esa recta el punto P.
Pero no tiene que ser únicamente un punto, puede ser una recta o cualquier figura geométrica la que reflejemos al otro lado de la recta. En la imagen tenemos también un círculo con respecto al cual llevaremos a cabo una reflexión semejante que en geometría se llama inversión. En el interior del círculo podemos reflejar todos los puntos, líneas o figuras geométricas, que podamos dibujar en el exterior del mismo, para lo cual proyectaremos una figura exterior, punto por punto, hacia el interior del círculo siguiendo la regla ya descrita de que
$R^2=|\overline{OP}|\cdot |\overline{OP’}|$
Despejando
$|\overline{OP’}|=\frac{R^2 }{|\overline{OP}|} $
y esta relación ya nos recuerda mucho a $y=\frac{1}{x^2}$ que es la fórmula de una hipérbola en el plano, de ahí que a esta geometría se le llame geometría hiperbólica.
Supongamos ahora un segmento delimitado por los puntos A y B.
De esta forma, un segmento $\overline{AB}$ se convierte por inversión dentro del disco en un arco de circunferencia A’B’.
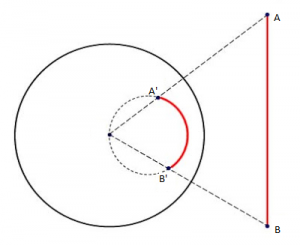
Es muy interesante ver que para que se forme una circunferencia completa dentro del disco, es necesario que la recta exterior se extienda hasta el infinito en ambas direcciones, cuyos extremos en el infinito tienden a «tocarse» justo en el centro del disco de Poincaré.
Dentro de la geometría hiperbólica definimos como «líneas paralelas» aquellas rectas infinitas trazadas dentro de un plano hiperbólico que no se cruzan jamás.
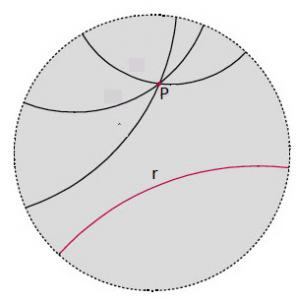
Las «rectas» hiperbólicas de color negro que se cortan en el punto P, aunque no son paralelas entre sí, son paralelas todas ellas a la «recta» hiperbólica de color rosa, lo cual significa que en una geometría hiperbólica, a través de un punto P externo a una recta dada, se pueden trazar infinitas rectas paralelas a la recta dada.
c) Por un punto exterior a una recta no pasa ninguna recta paralela a ella.
A esta geometría se le llama Geometría Elíptica, en donde sus rectas son rectas cerradas llamadas geodésicas. Tiene curvatura positiva. En la geometría elíptica, la suma de los ángulos de cualquier triángulo es siempre mayor a $180^{ \circ}$.
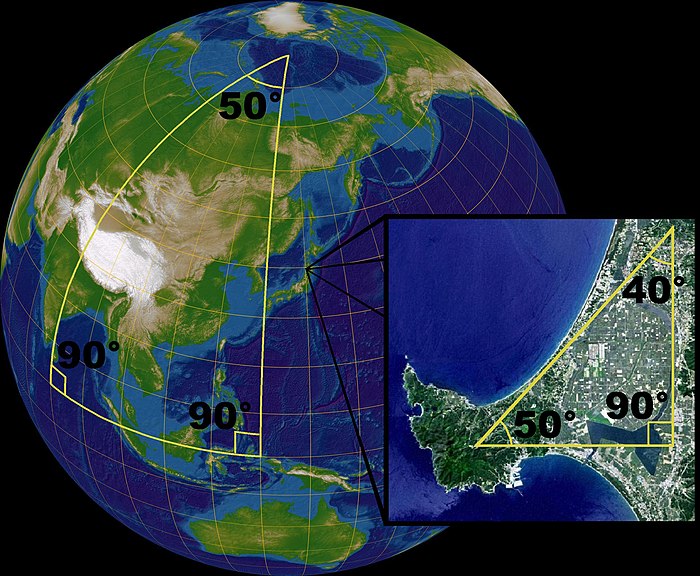
Esta geometría está basada en la superficie de un elipsoide. Un elipsoide es un sólido de revolución que se obtiene haciendo girar una elipse alrededor de uno de sus ejes de simetría. Por eso recibe el nombre de geometría elíptica y un caso particular de esta es la Geometría Esférica que se da por ejemplo en un globo o en la superficie de la Tierra. En esta geometría llamamos «plano» a la superficie de la esfera y «rectas» a las circunferencias de sus círculos máximos (¡ojo! Porque aquí está la clave de que no existan rectas paralelas). En esta geometría dos rectas siempre se cortan.
Si su centro es el punto $(x_0,y_0,z_0)$ y sus ejes son paralelos al de coordenadas, la ecuación del elipsoide es:
$\frac{{\left( {x – x_0 } \right)^2 }}{{a^2 }} + \frac{{\left( {y – y_0 } \right)^2 }}{{b^2 }} + \frac{{\left( {z – z_0 } \right)^2 }}{{c^2 }} = 1$
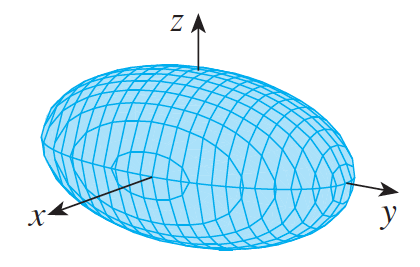
Cuando los semiejes a, b y c son todos iguales, entonces el elipsoide es una esfera.
Cuando el centro es el origen de coordenadas, la ecuación que deben satisfacer los puntos (x,y,z) para pertenecer a la esfera es:$x^2+y^2+z^2=r^2$ .
La geometría desarrollada sobre la superficie de un elipsoide aparte de ser conocida como geometría elíptica, también es conocida como geometría Riemmaniana, en honor al matemático Bernhard Riemman que impulsó este tipo de geometría.
Para terminar, un par de curiosidades:
La geometría no euclídea desarrollada por Bernhard Riemann es lo que hizo que Einstein pudiese dar a conocer al mundo su teoría de la Relatividad. Sin esas matemáticas, sin el mundo que esa geometría permitía, Einstein no hubiese podido desarrollar su teoría.
Para Newton la gravitación era una acción de fuerzas. Dos masas -por ejemplo, dos planetas esféricos- ejercen entre sí una fuerza que se transmite de uno a otro a lo largo de la recta imaginaria que pasa por sus centros. Para Einstein, sin embargo, la gravedad se debe a una curvatura del espacio-tiempo.
Para Einstein toda masa produce una curvatura en el espacio por el cual nosotros nos movemos/escurrimos. Imaginemos una sábana estirada y sujeta por sus esquinas colgando en el aire, ésta es una superficie euclidiana, es decir, una superficie plana. Si sobre esa sábana colocamos una pelota de tenis, esa superficie deja de ser plana para convertirse en curva. Cualquier objeto que se encuentre en la sábana, cerca de la pelota de tenis, se deslizará hacia ella por efecto de la curvatura. En el caso del espacio-tiempo, la Tierra, por ejemplo, curva nuestro espacio de forma que cuando soltamos de la mano cualquier objeto, esa curvatura hace que el objeto caiga hacia el suelo.
Es decir, según Einstein, la gravedad no es una fuerza, los cuerpos no tienen un efecto de atracción, sino que tienen un efecto de curvatura en la estructura del espacio-tiempo a su alrededor y cuanto más cerca de un cuerpo, mayor es la curvatura. Un objeto más pequeño no se acerca a uno más grande, sino que se mueve en la «inclinación» causada por el más grande.

